︎

Dougal Morrison




Reaction Diffusion and un-scientifically simulating Turing Patterns

Contributors/Authors        
Dougal Morrison




    Reaction-diffusion refers to a class of mathematical models that describe the dynamics of chemical reactions and the spatial spread of substances in a system.

    The interaction between reaction and diffusion processes gives rise to interesting and complex behaviors, such as the formation of spatial patterns, concentration gradients, and self-organization.

    One of the most famous examples of reaction-diffusion is the Turing pattern, proposed by the mathematician Alan Turing. His 1952 research paper titled, ‘The chemical basis of morphogenesis’ proposed a mechanism to explain the patterns observed in nature—the classic example being the striped pattern on a Zebra. Moreover, Turing noted that a unique property of biological systems is asymmetry.

︎︎︎










    In the context of Turing patterns in creative software such as Photoshop and After Effects the underlying concept of the ‘morphogen’ and ‘activator-inhibitor’ mechanism can be employed using features and effects within the software.

[1]    In biological systems the ‘morphogen’ would be molecules that emerge from a certain source in tissue. In PhotoShop, our morphogen is the pixel, more specifically, a cluster of pixels creating an initial shape. 

[2]    The ‘activator’ can be thought of as the component that introduces variations that contribute to the overall pattern formation.

[3]    The ‘inhibitor’ can be considered as the component that helps diffuse, spread and smooth the effects of the activator.







    Turing's mathematical analysis demonstrated that under certain conditions, an initially uniform distribution of signalling molecules or morphogens can spontaneously break symmetry and form distinct regions or domains with different concentrations. The formation of these patterns is a result of the interplay between two processes: an activator and an inhibitor.

    The activator enhances its own production and also promotes the production of the inhibitor. On the other hand, the inhibitor suppresses the production of both itself and the activator. Depending on the specific parameters of the system and combination of positive and negative feedback loops, a spatial instability arises...What results can be a variety of patterns, including spots, stripes, and labyrinths.



















Finding a set of corresponding tools/filters in Photoshop to Turin’s theoretical framework was the next step. The process I implemented in my experimentations are as follows:



Input

(Initial Shape/s)

︎︎︎

React/Activator

(High-Pass Filter, Threshold)

︎︎︎

Diffuse/Inhibitor

(Gaussian Blur/Directional Blur)

︎︎︎

Repeat
















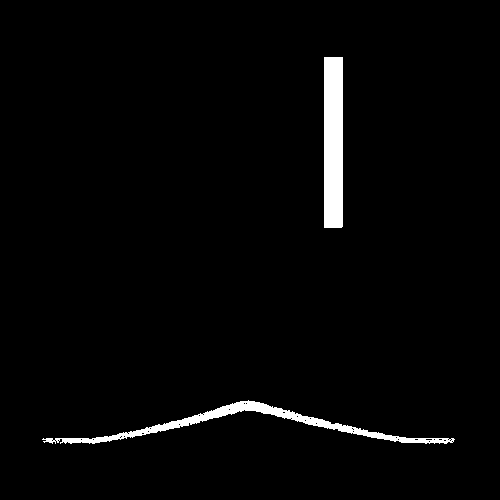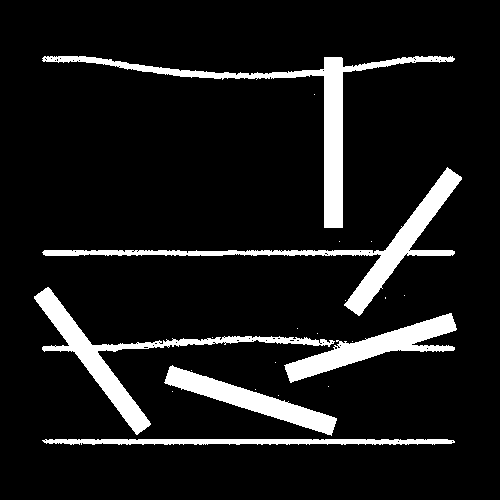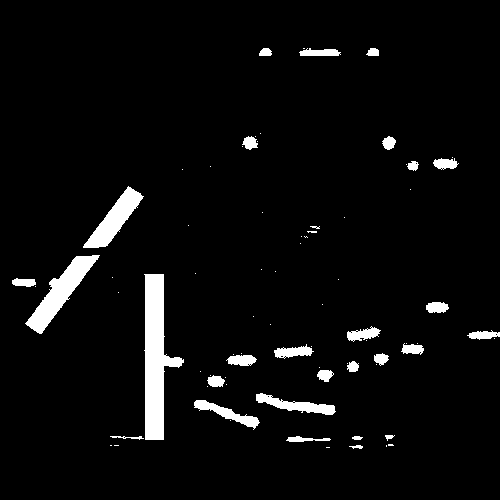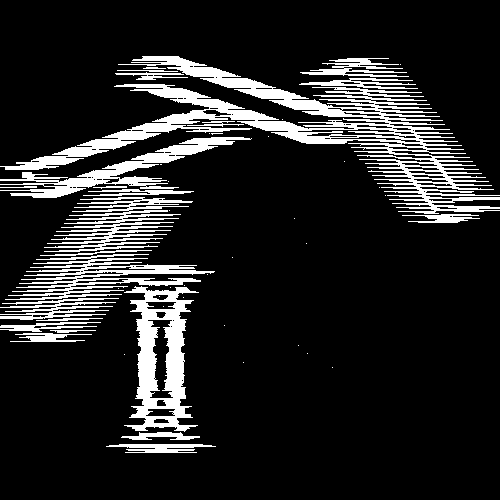
It is important to note that while these filters may be inspired by Turing patterns and the concept of an activator-inhibitor system, they are approximations designed using Photoshop and After Effects for creative purposes rather than precise scientific simulations.

 
Examples of creative software that can simulate accurate reaction-diffusion models include, Touch Designer and Houdini.






Further reading:

[1] Turing patterns, 70 years later. Nat Comput Sci 2, Pages 463–464 (2022). https://doi.org/10.1038/s43588-022-00306-0 

[2] Werth, Andrew. (2015). Turing Patterns in Photoshop. https://www.researchgate.net/publication/280626953_Turing_Patterns_in_Photoshop


 

© 2024